Το σύνολο Cantor και η τοπολογία του

1.1 Εισαγωγή

Το (τριαδικό) σύνολο Cantor το ανακάλυψε το 1874 ο H.J.S.Smith και το περιέγραψε ο ίδιος ο Cantor σε μια ηποσημείωση της εργασίας του πάνω στα τέλεια σύνολα[1], ως παράδειγμα μη πεπερασμένου, τέλειου συνόλου που δεν είναι πουθενά πυκνό[2]. Είναι ένα εξαιρετικά ενδιαφέρον μαθηματικό αντικείμενο και προκύπτει αρκετές φορές σε ένα πρόγραμμα προπτυχιακών σπουδών στα μαθηματικά , κυρίως σε μαθήματα ανάλυσης και θεωρίας συνόλων, αλλά σπάνια αποτελεί αντικείμενο πιο εκτεταμένης μελέτης. Σκοπός αυτού του άρθρου είναι να περιγράψει το σύνολο αυτό, την κατασκευή και συνοπτικά τις ιδιότητες του καθώς και τη γενίκευση του στη θεωρία συνόλων και στους τοπολογικούς χώρους.

1.2 Κατασκευή του συνόλου

Είναι δύσκολο να ορισθεί το σύνολο Cantor με τρόπο που είναι ταυτόχρονα μαθηματικά ακριβής και διαισθητικά χρήσιμος. Σχεδόν πάντα λοιπόν χρησιμοποιείται η εξής επαναληπτική κατασκευή:

1. Θεωρούμε το κλειστό διάστημα του πραγματικού άξωνα \(I=[0,1]\) και το γράφουμε σαν την ένωση τριών ίσων διαστημάτων \( [0,\frac{1}{3}]\cup(\frac{1}{3},\frac{2}{3})\cup[\frac{2}{3},1] \)
2. Αφαιρούμε το μεσαίο διάστημα \(\frac{2}{3}\) και έχουμε το σύνολο \(C_1 = [0,\frac{1}{3}]\cup[\frac{2}{3},1] \)
3. Αφαιρούμε το μεσαίο ανοικτό διάστημα από τα δύο διαστήματα τα οποία απαρτίζουν το \(C_1\) και έχουμε \(C_2 = [0,\frac{1}{9}]\cup[\frac{2}{9},\frac{1}{3}]\cup [\frac{2}{3},\frac{7}{9}]\cup[\frac{8}{9},1]\)
4. Συνεχίζουμε, αφαιρώντας το ανοικτό ενδιάμεσο διάστημα απο κάθε ένα απο τα τέσσερα κλειστά διαστήματα που απαρτίζουν το \(C_2\) ώστε να πάρουμε το \(C_3\)
5. Επαναλαμβάνουμε αυτή τη διαδικασία για κάθε βήμα \(n\in \mathbb{N}\) Αφαιρούμε δηλαδή τα ενδιάμεσα ανοικτά διαστήματα απο όλα τα κλειστά διαστήματα του \(C_n\) για να αποκτήσουμε το \(C_{n+1}\)
6. Το σύνολο του Cantor τελικά \(\bigcap_{n=1}^{\infty}C_n = C\)

Παρατήρηση : Για κάθε \(n\in \mathbb{N}\) το αντίστοιχο σύνολο \(C_n\) αποτελείτε απο \(2^n\) κλειστά διαστήματα ίσου μήκους.

Εδώ βρίσκεται μια οπτικοποίηση της γεωμετρικής κατασκευής του \(C_n,\) για \( n=1,2,3,…6\) :

Παρατηρούμε πως με διαδοχικές επαναλήψεις τις διαδικασίας που αναφέραμε πιο πάνω, το σύνολο τείνει, εκ πρώτης όψεως να είναι μια συλλογή απο άπειρες γραμμές οι οποίες έχουν προσεγγιστικά μηδενικό πλάτος ( ή μηδενικό μέτρο lebesgue όπως θα έλεγαν στη θεωρία μέτρου ). Ισχύει εάν παρατηρήσουμε τη μέθοδο κατασκευής του, πως το σύνολο Cantor δεν γίνεται να περιέχει κανένα διάστημα διότι του αφαιρέσαμε απο το \([0,1]\) (το οποίο σαφώς έχει μήκος 1) διαστήματα των οποίων το συνολικό μήκος τείνει στο 1. Έτσι οδηγούμαστε διαισθητικά στο συμπέρασμα πως το σύνολο Cantor περιέχει αποκλειστικά μονοσύνολα ή ακόμα πιο απλά, σημεία. Έύκολα καταλαβαίνουμε πως το σύνολο περιέχει άπειρα σημεία, μάλιστα για τον πληθάριθμο του ισχύει \(\left | C\right |=\left | [0,1]\right |=\left | R\right | \)] όπως θα δείξουμε παρακάτω. Επιπροσθέτως, δεν είναι πουθενά πυκνό. Συνεπώς, όχι μόνο το σύνολο έχει το ίδιο μέγεθος με το σύνολο απο το οποίο αφαιρέσαμε άπειρα στοιχεία για να το φτιάξουμε αλλά και ισχύει αυτό ενώ δεν περίεχει κανένα διάστημα και ενώ κανένα απο τα στοιχεία του δεν περιβάλεται πλήρως απο άλλα στοιχεία του!

1.3 Ιδιότητες

Δίνονται σχετικά μικρές αποδείξεις για κάποιες βασικές απο τις ιδιότητες του συνόλου. Οι αποδείξεις δεν είναι απαραίτητο να κατανοηθούν, μερικές απαιτούν γνώσεις απο τη θεωρία συνόλων, και μπορούν να παραληφθούν. Για όσους ενδιαφέροντε παραπάνω, οι περισσότερες υπάρχουν πιο επεξηγηματικά στα συγγράματα θεωρίας συνόλων. βλ. Δ.Γεωργίου – Σ. Ηλιάδης “Θεωρία Συνόλων” ,2η έκδοση σ.299 και R.W.Vallin “The Elements of Cantor Sets”, σ.21

1.3.1 Το \(C\) είναι μη-κενό

• Τετριμμένο. Παρατηρούμε πως υπάρχουν στοιχεία τα οποία δεν αφαιρούνται σε κανένα βήμα της κατασκευαστικής διαδικασίας. Για παράδειγμα τα άκρα του διαστήματος \([0,1]\).

1.3.2 Το \(C\) είναι φραγμένο

• Τετριμμένο. Εφόσον \(C\subset [0,1]\) για κάθε \(x \in C \Rightarrow x \in [0,1] \Rightarrow 0\leq x \leq 1\). Άρα φραγμένο με infimum το 1 και supremum το 0

1.3.3 Το \(C\) είναι κλειστό

• Είναι γνωστό πως στον το R με τη συνήθη τοπολογία που ορίζεται απο την ευκλείδια μετρική είναι τοπολογικός χώρος. Συνεπώς άπειρη ένωση ανοικτών συνόλων του είναι ανοικτό και πεπερασμένη τομή ανοικτών συνόλων του είναι ανοικτό. Αντίστοιχα, πεπερασμένη ένωση κλειστών συνόλων του είναι κλειστό και άπειρη τομή κλειστών συνόλων του είναι κλειστό. Στην κατασκευαστική διαδικασία είναι σαφές πως το \(C\) είναι άπειρη τομή κλειστών συνόλων και άρα επίσης κλειστό

Σημείωση: Απο τις παραπάνω δυο ιδιότητες παίρνουμε πως το \(C\) είναι συμπαγές διότι συμπαγές \(\equiv\) κλειστό και φραγμένο.

1.3.4 Το \(C\) δεν περιέχει κανένα διάστημα

Ισοδύναμα αποδεικνύουμε πως το συνολικό μήκος των διαστημάτων που αφαιρέσαμε απο το \([0,1]\) κατά τη διαδικασία κατασκευής είναι ίσο με 1 και άρα το \(C\) έχει μήκος 0 και συνεπώς δεν μπορεί να περιέχει κανένα διάστημα

• Στο n-οστό βήμα της κατασκευής έχουμε αφαιρέσει διαστήματα μήκους \(\Delta_n = \frac{1}{3} + \frac{2}{3^2} +\frac{4}{3^3} … + \frac{2^{n-1}}{3^n}= 1-(\frac{2}{3})^n\) και εύκολα βλέπουμε ότι το όριο αυτής της ακολουθίας καθώς \(n\to \infty\) ισούται με 1.

1.3.5 Το \(C\) είναι τέλειο σύνολο

Ορισμός: Ένα σύνολο \(X\) ονομάζεται τέλειο αν κάθε σημείο του είναι οριακό σημείο για κάποια ακολουθία με όρους άλλα στοιχεία του συνόλου. Δηλαδή αν για κάθε \(x \in X\) υπάρχει ακολουθία \(A_n\) τέτοια ώστε \( \lim A_n =x\) και \({A_n} \subset X\). Το\({Α_n}\) είναι γνήσιο υποσύνολο. Ισοδύναμα ένα σύνολο ονομάζεται τέλειο εάν είναι κλειστό και κάθε σημείο του είναι οριακό σημείο, αποδυκνείουμε αυτό.

Σημείωση: Παραδείγματα τέλειων συνόλων:

• Το κλειστό διάστημα [0,1] και γενικά κάθε κλειστό διάστημα
• Το R
• Το κενό

1.3.6 Το \(C\) δεν είναι πουθενά πυκνό *

*Η απόδειξη που δίνεται χρησιμοποιεί κάποιες βασικές έννοιες τοπολογίας, για τους περισσότερους σκοπούς όμως η διαισθητική ερμηνεία του ορισμού 3 αρκεί.

Ορισμός 1: Για ένα υποσύνολο \(X\) ενός τοπολογικού χώρου ( εδώ R) ορίζουμε την κλειστή του θήκη \(CL(X)\) ως το σύνολο των σημείων \(x\) του R για τα οποία ισχύει : για κάθε ανοικτό σύνολο \(U\) με \(x\in U\) έχουμε \(U\cap X \neq \emptyset\) .

Ορισμός 2: Για ένα υποσύνολο \(X\) ενός τοπολογικού χώρου ( εδώ R) ορίζουμε το εσωτερικό του \(Int(X)\) ως το σύνολο των σημείων \(x\) του R για τα οποία ισχύει : υπάρχει \(U\) ανοικτό σύνολο με \(x \in U\) τέτοιο ώστε \(U\subseteq X\) . Ισοδύναμα το \(Int(X)\) είναι ίσο με την ένωση όλων των ανοικτών υποσυνόλων του \(X\)

Ορισμός 3: Ένα σύνολο \(X\) είναι πουθενά πυκνό αν \(Int(CL(X)) = \emptyset \). Διαισθητικά αυτό σημαίνει πως τα στοιχεία του δεν είναι πουθενά “μαζεμένα μαζί”. Για παράδειγμα οι ακέραιοι είναι πουθενά πυκνοί στο R διότι μεταξύ οποιονδήποτε δύο ακεραίων έχουμε άπειρα στοιχεία. Αντίστροφα ένα διάστημα [a,b] στο R με \(a,b\in R\) είναι παντού πυκνό διότι τα στοιχεία του καλύπτουν όλο το ευθύγραμμο τμήμα μήκους 1 της πραγματικής γραμμής χωρίς κενά.

• Στην τοπολογία αποδεικνύεται πως εάν ένα σύνολο \(Χ\) είναι κλειστό ισχύει \(CL(X)=X\). Στην προκειμένη περίπτωση όπως δείξαμε το \(C\) είναι κλειστό άρα \(CL(C)=C\). Αρκεί άρα να δείξουμε πως η ένωση των ανοικτών υποσυνόλων του \(C\) είναι κενή. Ισοδύναμα, αφού ξέρουμε πως ένωση ανοικτών συνόλων είναι ανοικτό σύνολο, συνεπάγεται πως στο R ένωση ανοικτών συνόλων θα είναι ανοικτό διάστημα (a,b). Απο την ιδιότητα 1.3.4 γνωρίζουμε πως το \(C\) δεν περιέχει κανένα διάστημα και άρα το εσωτερικό του είναι κενό. Συνεπώς το \(C\) δεν είναι πουθενά πυκνό.

1.3.7 Το \(C\) είναι ολικά μη-συνεκτικό (totally disconnected)

Παντού μη-συνεκτικό διαισθητικά σημαίνει πως για οποιαδήποτε δύο σημεία \(x.y\in C\) μπορούμε να βρούμε ένα συνεχές μονοπάτι απο το \(x\) στο \(y\). Αυτό το μονοπάτι εφόσον βρισκόμαστε στο R σαφώς θα είναι ένα διάστημα. Απο την ιδιότητα 1.3.4 όμως γνωρίζουμε πως κανένα διάστημα δεν περιέχεται στο \(C\)

• Πιο αυστηρά: Έστω το σύνολο \(C_n\) για κάποιο βήμα n της διαδικασίας κατασκευής. Παρατηρούμε πως τα υποσύνολα που απαρτίζουν το \(C_n\) δεν συνδέονται μεταξύ τους, δηλαδή το \(C_n\) είναι ένωση ξένων διαστημάτων μήκους \(\frac{1}{3^{n-1}}\) το καθένα. Έστω \(x,y \in C\) τότε υπάρχει φυσικός \(N\) τέτοιος ώστε \(\frac{1}{3^{Ν-1}} < \left | x-y\right |\). Αυτό σημαίνε πως κατά το βήμα N τα \(x,y \) ανήκουν σε διαφορικά απο τα ξένα υποσύνολα που απαρτίζουν το \(C_n\) και συνεπώς δεν συνδέονται. Εφόσον αυτό ισχύει για οποιαδήποτε δύο στοιχεία του συνόλου Cantor, έχουμε πως είναι παντού μη-συνεκτικό.

1.3.8 Το \(C\) είναι υπεραριθμήσιμο

Ορισμός 1: Ένα σύνολο ονομάζεται πεπερασμένο εάν το πλήθος των στοιχείων του είναι πεπερασμένο. Ένα σύνολο ονομάζεται αριθμήσιμο εάν το πλήθος των στοιχείων του είναι άπειρο αλλά μπορεί να κατασκευαστεί μια 1-1 απεικόνιση απο το σύνολο αυτό στους φυσικούς αριθμούς. Διαισθητικά το πλήθος των στοιχείων του είναι ίσο με το πλήθος των φυσικών αριθμών

Ορισμός 2: Ένα σύνολο ονομάζεται υπεραριθμήσιμο εάν το πλήθος των στοιχείων του είναι άπειρο αλλά όχι αριθμήσιμο.

Σημείωση:Εάν φανταστούμε τους πραγματικούς αριθμούς, παρατηρούμε ότι μέσα τους περιέρχονται και οι άπειροι φυσικοί αριθμοί. Ανάμεσα όμως σε οποιουσδήποτε δύο φυσικούς αριθμούς παρεμβάλονται άπειροι άλλοι πραγματικοί αριθμοί. Διαισθητικά λοιπόν και πολύ πρόχειρα (και με καμία αυστηρότητα) μπορούμε να πούμε πως η απειρία των πραγματικών αριθμών είναι πολύ μεγαλύτερη απο την απειρία των φυσικών ή ότι οι πραγματικοί αριθμοί απειρίζονται με διαφορετικό τρόπο απο τους φυσικούς.

Παραδείγματα:

1. Το σύνολο των στοιχείων της ακολουθίας \(\frac{1}{n}\) με \(n\) να διατρέχει τους φυσικούς είναι αριθμήσιμο. Εύκολα βλέπουμε πως μια 1-1 απεικόνιση απο αυτό στους φυσικούς κατασκευάζεται έτσι:
   \(1\mapsto \frac{1}{1}\)
   \(2\mapsto \frac{1}{2}\)
   \(3\mapsto \frac{1}{3}\)
   .
   .
   .
   \(n\mapsto \frac{1}{n}\)
   
2. Το σύνολο (0,1) είναι υπεραριθμήσιμo
3. Οι ρητοί είναι αριθμήσιμοι
4. Το σύνολο των ακεραίων είναι αριθμήσιμο αφού υπάρχει 1-1 αντιστοιχία με τους φυσικούς όπως φαίνεται στην εικόνα

Ιδιότητες: Έστω \(X,Y\) δύο σύνολα

1. Αν \(X\) υπεραριθμήσιμο και \(X \subset Y\) τότε το \(Y\) υπεραριθμήσιμο
2. Αν \(X\) υπεραριθμήσιμο τότε \(X\cup Y\) υπεραριθμήσιμο ανεξάρτητα του \(Y\)
3. Αν \(X\) υπεραριθμήσιμο τότε \(X\times Y\) υπεραριθμήσιμο ανεξάρτητα του \(Y\)
4. Αν \(X\) άπειρο ( είτε αριθμήσιμο είτε όχι) τότε \(P(X)\) υπεραριθμήσιμο

• Η απόδειξη παραλείπεται. Η κλασική απόδειξη της πρότασης αυτής γίνεται με το διαγώνιο επιχείρημα του Cantor και βασίζεται στην βάση-3 αριθμητική.

Σημείωση: Στη θεωρία συνόλων εύκολα αποδεικνύεται πως κάθε υπεραριθμήσιμο σύνολο έχει τον ίδιο πληθάριθμο \(2^{\aleph_0
}\) όπου \(\aleph_0\) (άλεφ μηδέν) ο πληθάριθμος των φυσικών. \(2^{\aleph_0
}\) είναι επίσης ο πληθάριθμος του δυναμοσυνόλου των φυσικών. Τελικά απο τα παραπάνω καταλήγουμε πως \(\left | C\right | = \left | [0,1]\right |=\left | R\right |\) και γενικά οποιοδήποτε κλειστό ή ανοικτό υποδιάστημα του R έχει ίδιο πληθάριθμο με το ίδιο το R.

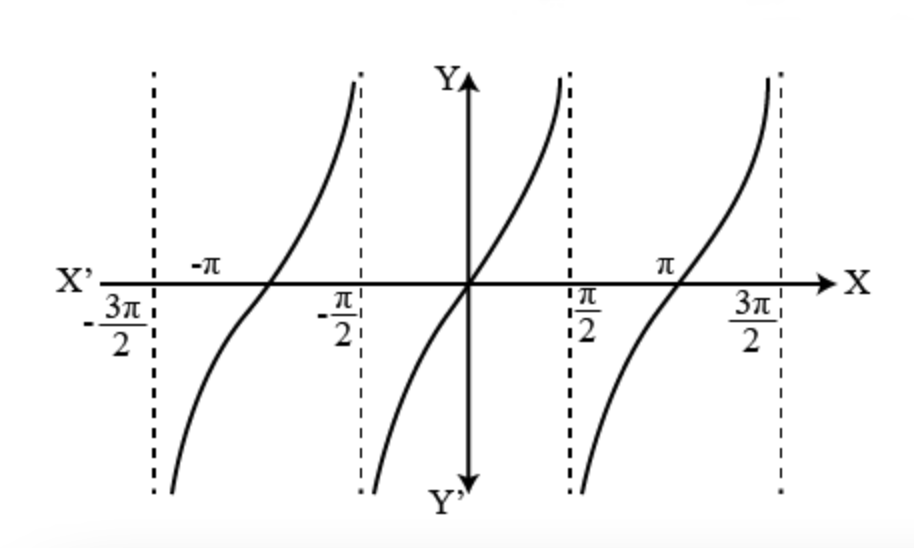
Για παράδειγμα το ανοικτό διάστημα \(\left ( \frac{-\pi}{2},\frac{\pi}{2} \right )\) έχει ίδιο πληθάριθμο με το R αφού η απεικόνιση \(f(x)=tanx\) με πεδίο ορισμού το \(\left ( \frac{-\pi}{2},\frac{\pi}{2} \right )\) είναι 1-1 και η εικόνα της είναι όλο το R όπως φαίνεται στην εικόνα

Έως τώρα έγινε ο ορισμός, η κατασκευή και οι αποδείξεις των βασικών ιδιοτήτων του τριαδικού συνόλου Cantor. Υπάρχει όμως και μια γενική οικογένεια συνόλων Cantor που επιδεικνύουν παρόμοια συμπεριφορά και κατασκευάζονται με παρόμοιο τρόπο. Συγκεκριμένα για ένα οποιοδήποτε σύνολο ισχύει:

• Είναι κλειστό
• Είναι φραγμένο
• Είναι ολικά μη-συνεκτικό (totally disconnected)
• Είναι τέλειο

Τότε αυτό ανοίκει στην οικογένεια των συνόλων Cantor (ή απλά ονομάζεται σύνολο Cantor). Υπάρχουν πάρα πολλά γνωστά σύνολα Cantor, κάποια προκύπτουν με προφανείς τρόπους κάνωντας αλλαγές στη διαδικασία κατασκευής (όπως αυτά που θα δείξουμε εδώ) και κάποια όχι. Επίσης κάποια είναι τοπολογικά ομόμορφα με το τριαδικό σύνολο Cantor (αυτά ονομάζονται χώροι Cantor) και κάποια όχι. Θα δούμε δύο παραδείγματα

Μεσαίο 1/5 σύνολο Cantor

Όπως φαίνεται για να φτιάξουμε το “μεσαίο 1/5 σύνολο Cantor” = \(C_5\) ακολουθούμε την ίδια ακριβώς κατασκευαστική διαδικασία όπως με το τριαδικό σύνολο, απλά αντι να αφαιρούμε σε κάθε βήμα το μεσαίο 1/3 κάθε υποσυνόλου, αφαιρούμε το μεσαίο 1/5.

1. Απο το κλειστό διάστημα [0,1] αφαιρούμε το ανοικτό μεσαίο διάστημα μήκους 1/5. Δηλαδή το διάστημα \(\left ( \frac{2}{5},\frac{3}{5} \right )\). Και έχουμε το διάστημα \(K_1=\left [ 0,\frac{2}{5} \right ]\cup \left [ \frac{3}{5},1 \right ]\)
2. Συνεχίζουμε αφαιρόντας το μεσαίο 1/5 απο το καθένα απο τα ξένα κλειστά διαστήματα που αποτελούν το \(K_1\) και παίρνουμε το διάστημα \(K_2\) = \(\left [ 0,\frac{4}{25} \right ]\cup \left [ \frac{6}{25},\frac{2}{5} \right ]\cup \left [ \frac{3}{5},\frac{19}{25} \right ]\cup \left [ \frac{21}{25},1 \right ]\)
3. Συνεχίζουμε τη διαδικασία για άπειρο αριθμό επαναλήψεων και τελικά έχουμε \(K_n = C_5\) καθώς \(n\to \infty\)

Παρατηρούμε πως όπως και πριν, στο n-οστό βήμα, αφαιρούμε \(2^{n-1}\) ξένα και ανοικτά υποσύνολα απο το \(K_{n-1}\), η διαφορά τώρα είναι πως το καθένα απο αυτά θα έχει μήκος \(5^{-n}\). Δηλαδή για το μέτρο \(L_{n}\) που μας απομένει σε κάθε βήμα επανάληψης έχουμε: \(L_{1}=\frac{4}{5}\), \(L_{2}= \frac{4^2}{5^2}\), \(L_{3}= \frac{4^3}{5^3}…\) και τελικά \(L_{n}\) = 0 καθώς \(n\to \infty\). Δηλαδή αποδείξαμε πως το μέτρο του \(C_5\) είναι 0 και άρα δεν περιέχει κανένα διάστημα. Με αντίστοιχο τρόπο μπορούμε να δείξουμε και τις άλλες ιδιότητες οι οποίες, εν προκειμένω ισχύουν όλες.

Σημείωση: Τα δύο σύνολα που παρουσιάστηκαν έως τώρα, δημιουργούνται απο την άπειρη ένωση αριθμήσιμου πλήθους κλειστών διαστημάτων, ως εκ τούτου είναι και σύνολα Borel

Το Smith-Volterra Σύνολο Cantor (ε – Σύνολο Cantor)

To Smith-Volterra Σύνολο Cantor (SVC) είναι ίσως το πρώτο σύνολο Cantor που δημοσιεύτηκε. Συζητήθηκε πρώτη φορά σαν ιδέα το 1875 και εκδόθηκε πρώτη φορά το 1881 ( ενώ το τριαδικό σύνολο Cantor το 1883). Επίσης, σε αντίθεση με τα όσα παρουσιάστηκαν μέχρι τώρα, ενώ όπως και τα προηγούμενα σύνολα, δεν είναι πουθενά πυκνό (δεν περιέχει κανένα διάστημα) έχει θετικό και όχι μηδενικό μέτρο. Τα σύνολα της οικογένειας Cantor που έχουν αυτή την ιδιότητα, ονομάζονται χοντρά σύνολα Cantor (fat Cantor sets)

Σημείωση: Παραπάνω είπαμε πως ένα σύνολο μηδενικού μέτρου δεν μπορεί να περιέχει διαστήματα, το αντίστροφο δεν ισχύει. Δηλαδή δεν είναι απαραίτητο πως ένα σύνολο μη-μηδενικού μέτρου, θα περιέχει κάποιο διάστημα.

Η διαδικασία κατασκευής είναι παρόμοια με τις προηγούμενες, δηλαδή ξεκινάμε με το διάστημα [0,1] και αφαιρούμε ανοικτά υποδιαστήματα τους σε κάθε βήμα, διαφέρει όμως σημαντικά ως προς τις αναλογίες των διαστημάτων που αφαιρούνται. Για το κλασικό \(C\) σε κάθε βήμα αφαιρούσαμε το μεσαίο 1/3 απο κάθε υποδιάστημα, ο λόγος δηλαδή του μήκους του αφαιρούμενου ανοικτού διαστήματος προς το μέτρο του υποδιαστήματος στο οποίο ανήκει, έμενε σταθερός σε κάθε επαναληπτικό βήμα. Παρομοίως και για το μεσαίο 1/5 σύνολο (και αντίστοιχα για το μεσαίο 1/7 σύνολο Cantor κ.ο.κ.) Αυτό νομοτελειακά θα οδηγήσει σε σύνολα μέτρου μηδέν, τώρα όμως για το \(SVC\) καθώς και γενικά για όλα τα χοντρά σύνολα Cantor ο λόγος μέτρου των αφαιρούμενων ανοικτών διαστημάτων προς το μέτρο του υποδιαστήματος στο οποίο ανήκουν, δεν παραμένει σταθερός αλλά σε κάθε βήμα μειώνεται. Αυτή η διαφορά είναι που μας οδηγεί σε σύνολα της οικογένειας Cantor με μη-μηδενικό μέτρο.

Για τη διαδικασία κατασκευή του \(SVC\) έχουμε:

• Ξεκινάμε ξανά με το διάστημα [0,1]
• Αφαιρούμε το μεσαίο \(\frac{1}{4}\) του διαστήματος και έχουμε το \(SVC_1=\left [ 0,\frac{3}{8} \right ]\cup \left [ \frac{5}{8},1 \right ]\)
• Απο τα εναπομείναντα 2 κλειστά υποδιαστήματα αφαιρούμε το μεσαίο \(\frac{1}{4^2}\) τους και έχουμε \(SVC_2=\left [ 0,\frac{5}{32} \right ]\cup \left [ \frac{7}{32},\frac{3}{8} \right ]\cup \left [ \frac{5}{8},\frac{25}{32} \right ]\cup \left [ \frac{27}{32},1 \right ]\)
• Επαγωγικά συνεχίζουμε αφαιρώντας το μεσαίο ανοικτό υποδιάστημα μήκους \(\frac{1}{4^n}\) απο καθένα απο τα εναπομείναντα \(2^{n-1}\) κλειστά υποδιαστήματα για να κατασκευάσουμε το n\mapsto \infty.
• Τελικά το σύνολο μας \(SVC\) είναι το \(SVC_n\) καθώς \(n\mapsto \infty\)

Παρατηρούμε πως όπως αναφέρθηκε και πιο πάνω, ο λόγος του μέτρου του αφαιρούμενου υποδιαστήματος και του μέτρου του διαστήματος στο οποίο ανήκει, μεταβάλεται σε κάθε επαναληπτικό βήμα. Αυτό ισχύει γενικά για τις κατασκευές όλων των χοντρών συνόλων Cantor. Στη συγκεκριμένη περίπτωση για το μέτρο των υποδιαστημάτων του \([0,1]\) που αφαιρέσαμε έχουμε:

\( \sum_{0}^{\infty}\frac{2^n}{2^{2n+2}} = \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} … = \frac{1}{2}\)

άρα τελικά το μέτρο του \(SVC=1-\frac{1}{2}=\frac{1}{2}\)

Το \(SVC\) είναι σύνολο Cantor όμως όπως είδαμε δεν μοιράζεται απαραίτητα όλες τις ιδιότητες του τριαδικού συνόλου, αφού δεν έχει μέτρο 0.