Το άρθρο αυτό αποτελεί μια μικρή εισαγωγή στα κυτταρικά αυτόματα με σκοπό τα επόμενο άρθρα να μπορέσουν να παρουσιάσουν ενδιαφέρουσες συμπεριφορές αυτών κυρίως όταν αυτές είναι χαοτικές ή όταν μέσα από αυτές αναδύονται φράκταλς.
Τα κυτταρικά αυτόματα (cellular automata – εφεξής CA) μελετήθηκαν πρώτη φορά τη δεκαετία του ’40 από τους John von Neumann και Stanislaw Ulam. Έγιναν γνωστά όμως απο τη δουλειά του John Conway έτσι όπως παρουσιάστηκε μέσα από τα άρθρα του Steven Gardener και έκτοτε παραμένουν σταθερό ενδιαφέρον των μαθηματικών. Αποτελούν μια ειδική περίπτωση δυναμικού συστήματος.
Δυναμικό σύστημα ονομάζεται οποιοδήποτε σύστημα εξαρτάται από τον χρόνο. Ένα ρευστό το οποίο εκτελεί κάποια κίνηση, ένα εκρεμές, οι λύσεις μιας οικογένειας διαφορικών εξισώσεων \(f_{n}(t)\), μπορούν να αναπρασταθούν ως δυναμικά συστήματα. Για να περιγράψουμε λοιπόν ένα δυναμικό σύστημα, χρειάζεται καταρχάς να έχουμε έναν κανόνα ο οποίος μας περιγράφει πως συμπεριφέρεται το σύστημα μας καθώς κυλάει ο χρόνος. Έπειτα, χρειάζομαστε έναν χώρο για τον οποίο ισχύει πως κάθε πιθανή κατάσταση του συστήματος αντιστοιχεί σε ένα σημείο του. Ο χώρος αυτός ονομάζεται χώρος των φάσεων.
Οι κανόνες, οι χώροι των φάσεων αλλά ακόμα και το πως μετράμε τη χρονική παράμετρο του συστήματος διαφέρουν ποιοτικά ανάλογα με το σύστημα το εκάστοτε σύστημα. Πράγματι, εάν για παράδειγμα μοντελοποιούμε την κίνηση ενός σωματιδίου μέσα σε ένα δοχείο για 1 λεπτό, θα χρειαστούμε και έναν αντίστοιχο χώρο τριών διαστάσεων ικανό να περιγράψει οποιαδήποτε θέση του σωματιδίου. Επίσης παρατηρούμε πως η χρονική παράμετρος \(t\) ανήκει σε στο συνεχές διάστημα \((0,60)\) το οποίο είναι υποσύνολο του πραγματικού άξονα. Αντίθετα, εάν θέλουμε να μοντελοποιήσουμε τον πληθυσμό ενός είδους θα πρέπει να στήσουμε και το αντίστοιχο δυναμικό σύστημα. Ας πούμε πως ανά χρόνο \(t_1\) ο πληθυσμός \(P(t)\) διπλασιάζεται. Δηλαδή για \(t=0\) έχουμε P=\(x_0\), για \(t=t_1\) έχουμε \(P=2x_0\), για \(t=2t_1\) έχουμε \(P=4x_0\)…
Άμεσα βλέπουμε πως δεν χρειαζόμαστε παρά έναν συνεχή άξονα για να περιγράψουμε τον πληθυσμό. Επίσης βλέπουμε πως η χρονική παράμετρος δεν ανήκει σε κάποιο συνεχές διάστημα αλλά σε ένα διακριτό σύνολο της μορφής \( { 0,t_1,t_2,t_3,…}\), είναι δηλαδή διακριτή παράμετρος. Ένα τελευταίο παράδειμα μπορεί είναι το να σκεφτούμε ένα μικρόβιο σε κάποια επιφάνεια και να μοντελοποίησουμε το αν αυτό το μικρόβιο θα είναι ζωντανό ή όχι οποιαδήποτε χρονική στιγμή. Ας πούμε ότι ο κανόνας μας είναι ο εξής: Το μικρόβιο είναι ζωντανό για \(t<t_1\), αλλιώς είναι νεκρό. Το σύστημα αυτό έχει μόνο δύο πιθανές καταστάσεις, ζωνταντό και νεκρό. Ο χώρος φάσεων του δηλαδή είναι διακριτός ενώ αντίθετα η χρονική παράμετρος είναι συνεχής.
Έτσι περιγράψαμε πολύ απλά μερικές από τις βασικές κατηγορίες δυναμικών συστημάτων. Δηλαδή, δυναμικά συστήματα συνεχούς χώρου και χρόνου, δυναμικά συστήματα συνεχούς χώρου αλλά διακριτού χρόνου και δυναμικά συστήματα διακριτού χώρου αλλά συνεχούς χρόνου. Το άρθρο αυτό, απασχολείται με την τέταρτη και τελευταία κατηγορία, αυτή των δυναμικών συστημάτων διακριτού χώρου και διακριτού χρόνου.
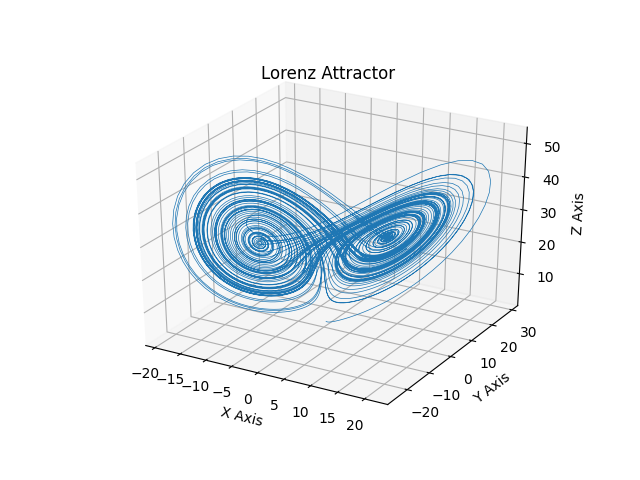
Ο ελκυστής του Lorenz. Είναι ένα σύνολο λύσεων του συστήματος Lorenz το οποίο είναι ένα σύστημα συνήθων διαφορικών εξισώσεων. Έχουμε συνεχή χώρο και συνεχή χρόνο.
Μια αρκετά απλή αλλά αρκετά ενδιαφέρουσα περίπτωση συστήματος διακριτού χώρου και χρόνου αποτελούν τα κυτταρικά αυτόματα. Η αναπαράσταση του χώρου των CA είναι εξαιρετικά απλή, ένα επίπεδο χωρισμένο σε ίσα τετράγωνα. Κάθε τετράγωνο αποτελεί ένα κύτταρο (cell) και σκοπός μας είναι να μοντελοποίησουμε την κατάσταση κάθε κυττάρου και το πως αυτή αλλάζει ανάλογα με την χρόνο. Επομένως το επόμενο που θα πρέπει να κάνουμε είναι να καθορίσουμε τις πιθανές καταστάσεις που μπορεί να έχει ένα κύτταρο. Αυτές μπορεί να είναι όποιες επιθυμούμε και όσες επιθυμούμε αρκεί το σύνολο τους να είναι πεπερασμένο. Για παράδειγμα μπορεί το σύνολο των δυνατών καταστάσεων για κάθε cell στο σύστημα μας να είναι {ζωντανό,νεκρό} ή {μωβ,πράσινο,κόκκινο} ή {1,2,3….n}. Έπειτα χρειάζεται να προσδιορίσουμε την γειτονιά ενός κυττάρου ώστε έπειτα με βάση αυτή να ορίσουμε τον κανόνα του συυστήματος μας. H γειτονιά ενός κυττάρου μπορεί να οριστεί όπως επιθυμούμε εμείς αρκεί να ορίζεται με τον ίδιο τρόπο για κάθε κύτταρο. Για παράδειγμα σε ένα σύστημα μπορεί να θεωρήσουμε ότι γειτονιά ενός κυττάρου είναι {το κύτταρο που βρίσκεται στα αριστερά του + το κύτταρο που βρίσκεται στα δεξιά του}, σε ένα άλλο σύστημα μπορεί να θεωρήσουμε ότι είναι {τα πρώτα 4 κύτταρα που βρίσκονται πάνω διαγώνια και προς τα αριστερά του κυττάρου} ή οτιδήποτε άλλο μπορούμε να σκεφτούμε. Οι δύο πιο κλασικές γειτονίες που χρησιμοποιούνται συχνά είναι αυτές των von Neumann και Moore οι οποίες φαίνονται εδώ
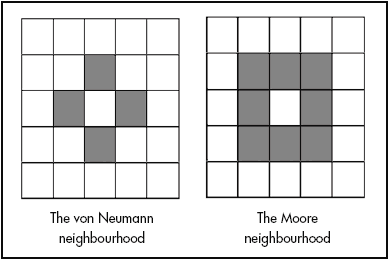
Οι γειτονιές von Neumann και Moore. Παρατηρούμε πως κάθε κύτταρο αποτελεί μέρος της γειτονιάς άλλων κυττάρων
Έχουμε πλέον ορίσει τον χώρο,τα κύτταρα, τις καταστάσεις και τις γειτονιές, χρειάζεται να ορίσουμε και έναν κανόνα, βάσει του οποίου τα κύτταρα μας θα αλλάζουν κατάσταση. Ο κανόνας, ξανά, μπορεί να είναι ό,τι θέλουμε εμείς να είναι. Για παράδειγμα εάν οι πιθανές μας καταστάσεις είναι {νεκρό,ζωνταντό}, η γειτονιά μας είναι η γειτονιά του Moore μπορούμε να ορίσουμε τον κανόνα “Αν το κύτταρο είναι νεκρό, παραμένει νεκρό. Αν το κύτταρο είναι ζωντανό και τουλάχιστον τέσσερα κύτταρα της γειτονιάς του είναι ζωντανά, το κύτταρο παραμένει ζωνταντό, αλλιώς γίνεται νεκρό” έχουμε ορίσει πλήρως το σύστημα μας και η διαδικασία (η οποία είναι επαναληπτική διότι δουλεύουμε σε διακριτό χρόνο) του έχει ως εξής:
- Ορίζουμε κάποιες αρχικές συνθήκες, δηλαδή στην αρχή της μοντελοποίησης μας, ποιά κύτταρα θα είναι νεκρά και ποιά ζωνταντά
- Για κάθε κύτταρο ξεχωριστά, με βάση τον κανόνα και την κατάσταση των κυττάρων της γειτονιάς του, υπολογίζουμε ποιά κατάσταση θα πρέπει να πάρει
- Ανανεώνουμε όλα τα κύτταρα μαζί. Εδώ τελειώνει η πρώτη επανάληψη (δηλαδή 1 μονάδα χρόνου = 1 επανάληψη)
- Επαναλαμβάνουμε τα παραπάνω βήματα \(n\) φορές ώστε να έχουμε \(n\) επαναλήψεις
Τα παραπάνω μπορούν να κωδικοποιηθούν πιό αυστηρά μέσα από τις εξής σχέσεις, οι παράμετροι των οποίων ορίζουν ένα σύστημα όπως εξηγήσαμε παραπάνω:
- Θεωρούμε ένα πλέγμα ίσων τετραγόνων \(m\times m\) διάστασης ή άπειρης διάστασης
- Σε κάθε επανάληψη (διακριτό χρονικό βήμα) κάθε κύτταρο βρίσκεται σε ακριβώς μία κατάσταση \(s\in S\) όπου \(\left | S\right | \in N\)
- Η συμπεριφορά οποιουδήποτε κυττάρου εξαρτάται αποκλειστικά και μόνο από την κατάσταση των κυττάρων της γειτονιάς του
- Σε κάθε βήμα κάθε κύτταρο ανανεώνει την κατάσταση του σύμφωνα με μια ντερεμινιστική απεικόνιση \(\phi: S^n\mapsto S\) που απεικονίζει τις \(n\) καταστάσεις της γειτονιάς του κυττάρου στο σύνολο των καταστάσεων \(S\)
- Η ανανέωση της κατάστασης κάθε κυττάρου γίνεται ταυτόχρονα με την ανανέωση όλων των άλλων
Όλα αυτά ίσως διαβάζουν λίγο αφηρημένα οπότε ας δούμε μερικά απλά παραδείγματα τα οποία τρέχουν στο πρόγραμμα Golly, το σύνηθες περιβάλλον για πειραματισμό και έρευνα στα CA (επίσης χρησιμοποιείται αρκετά και η mathematica που είναι περισσότερο εύχρηστη αλλά και πιό περιορισμένη)
